How to Implement Stack in C++? Amortized analysis

What is a Stack? permalink

A stack is a linear data structure, that follows the LIFO (last-in, first-out) principle. As the acronym suggets, the most recent element that enters the stack via a method called push() is the first that exits or pops out of the data structure.

The concept of this DS is pretty simple to grasp. We can think of it as a real-life stack of books (if you’re one of those who still reads physical books).

The book that is in the top of the stack is the first one you pick.

To get to the book at the bottom of the stack, you need to go through all elements of the stack, popping them until you arrive at the first book.

We use stacks in all fields of programming. From solving competitive programming problems, to using them to perform recursive calls.

Enough talk, let’s see how to implement a stack in C++ from scratch. Of course, you can use the stack data structure defined in the standard library, but the following is for mere learning purposes.

Implementing a Stack in C++ permalink

Let’s first define the methods of the stack:

• top(): Returns the element at the top of the stack
• push(): Inserts an element at the top of the stack.
• pop(): Takes out the element at the top of the stack and returns it.
• size(): Returns an integer, the number of elements the stack currently stores.
• empty(): You guessed it! Returns a boolean indicating if the stack is empty or not.

We’ll use a dynamic array to implement the Stack. Imagine having to define a fixed size for the stack and then running out of space. A stack should be inherently dynamic.

We should also be able to create a stack of chars, strings, and even other stacks. In general, the stack must be able to store any other data-structure. We’ll do that with C++ function templates.

Let’s start by importing the libraries we need, in this case only <iostream>. I’ll also use the std namespace.

#include <iostream>
using namespace std;

Now, let’s create a struct inside a function template called Stack.

template<typename T> struct Stack{
  int _top, capacity;
  T* data;

  Stack(){
    _top = 0; 
    capacity = 16;
    data = new T[capacity];
  }

  ...
}

As you can see we only have three main attributes:

• _top: The index of the current top element.
• capacity: The current capacity of the dynamic array.
• data: A pointer to an array of type T.

The whole idea of the implementation is to have a dynamic array of type T, and the index of the current top element off by one. We define it to be always be one index off the actual top element because this makes the implementation of the following methods easier.

Creating the auxiliary methods:

  ...
  bool empty(){
    return _top == 0;
  }

  int size(){
    return _top;
  }
  
  T top(){
    if (empty()){
      throw "Stack is empty!";
    }
    return data[_top - 1];
  }

We throw an exception in case there is nothing to top.

Now the core of this implementation, the push() and top() methods.

  ...
  void push(T element){
    if (size() == capacity){
      // create new array
      capacity *= 2;
      T* new_arr = new T[capacity];
      // Copy elements from data to new array
      for (int i = 0; i < size(); i++){
        new_arr[i] = data[i];
      }

      swap(data, new_arr);
      delete [] new_arr;
    }
    data[_top++] = element; 
  }

  T pop(){
    if (empty()){
      throw "Stack is empty!";
    }
    return data[--_top];
  }

We create another array of type T with double the capacity of the current array. Then we copy all the elements from the current array to the new array, swap them out, and free the space of the old array before inserting the element we initially desired to push.

Note how every time we call the code inside the condition, we run n operations by copying the elements of the previous array to the new one. We’ll later see why this doesn’t affect the overall $O(1)$ complexity of push().

Full implementation permalink

Here’s the full code of the stack in c++;

#include <iostream>
using namespace std;

template<typename T> struct Stack{
  int _top, capacity;
  T* data;

  Stack(){
    _top = 0; 
    capacity = 16;
    data = new T[capacity];
  }

  bool empty(){
    return _top == 0;
  }

  int size(){
    return _top;
  }
  
  T top(){
    if (empty()){
      throw "Stack is empty!";
    }
    return data[_top - 1];
  }
  
  void push(T element){
    if (size() == capacity){
      // create new array
      capacity *= 2;
      T* new_arr = new T[capacity];
      // Copy elements from data to new array
      for (int i = 0; i < size(); i++){
        new_arr[i] = data[i];
      }

      swap(data, new_arr);
      delete [] new_arr;
    }
    data[_top++] = element; 
  }

  T pop(){
    if (empty()){
      throw "Stack is empty!";
    }
    return data[--_top];
  }
};

Amortized analysis: Why pushing is $O(1)$ permalink

The key of why pushing into a stack, and in general any dynamic array is an $O(1)$ operation lies on the frequency we copy over the elements from one array to a new one with more capacity.

The observation is that we perform the array resize as our input increases to every power of 2.

In general, for an input size of n we perform $\log_{2}(n)$ resizes. For each one of these array resizes we make n copies of elements from the current array to a new one.

We’re left with the following equation:

The only strange thing is the summation formula up in the numerator. It represents the number of operations we make when resizing the array every $log_2(jn)$ times. Of course, this summation has an asymptotic limit of $O(n)$

This algorithmic analysis technique is called agreggate method.

I made the following C++ script using the stack implementation shown above. Basically we insert n elements into the stack.

int main(){
  int n; cin >> n;
  Stack<int> s;
  for (int i =0 ;i < n; i++){
    s.push(i);
  }
  return 0;
}

We can peek at the performance of the push() method as n increases up to $10^5$ in the following plot.

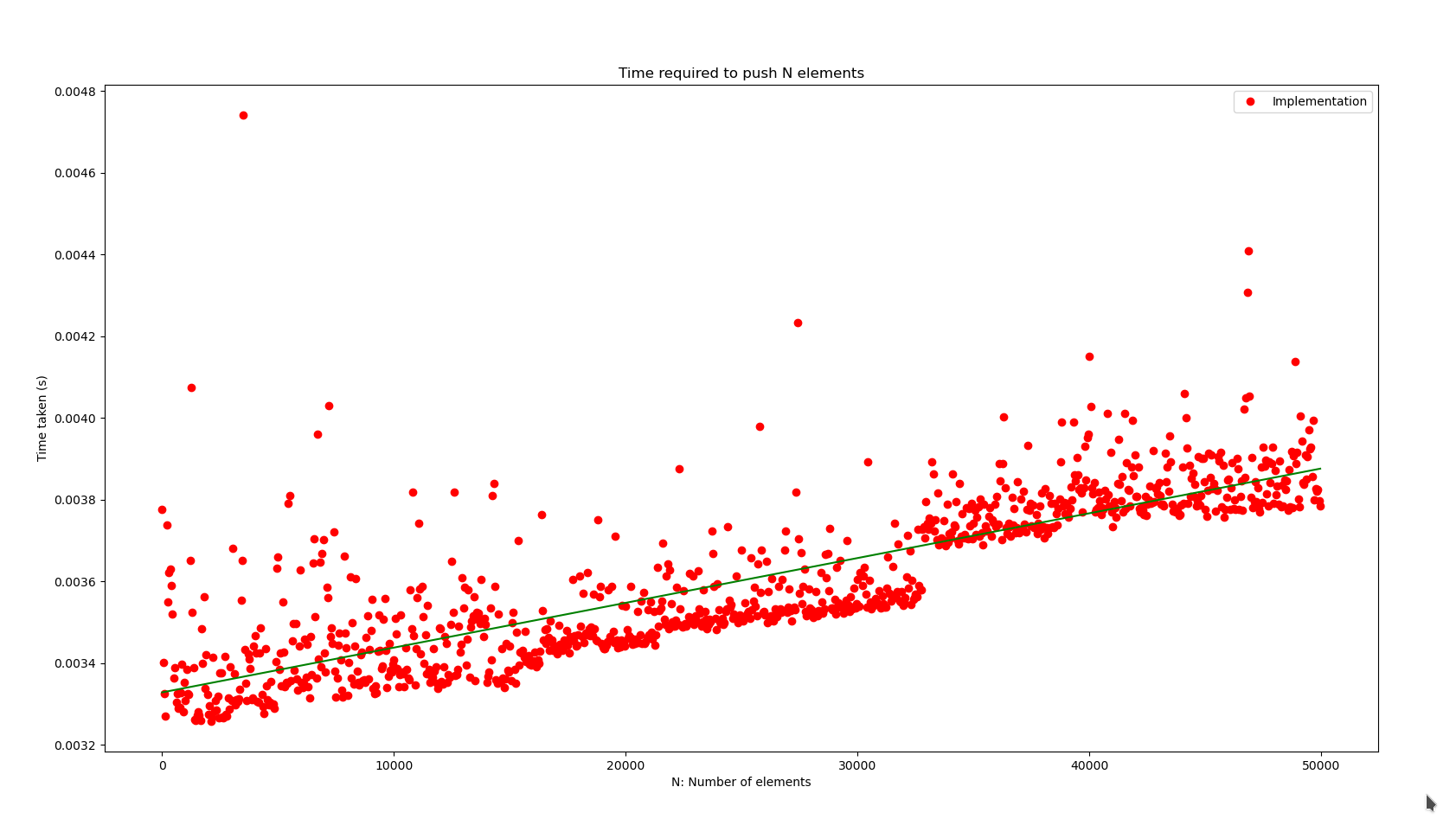
Here the green line represents a function of the form $f(x) = mx + b$ .

In general we observe the behavior of the algorithm as a linear function depending on n. But because we’re doing n operations we get that the complexity of the push() method is:

We can also compare our implementation with the one declared in the C++ standard library.

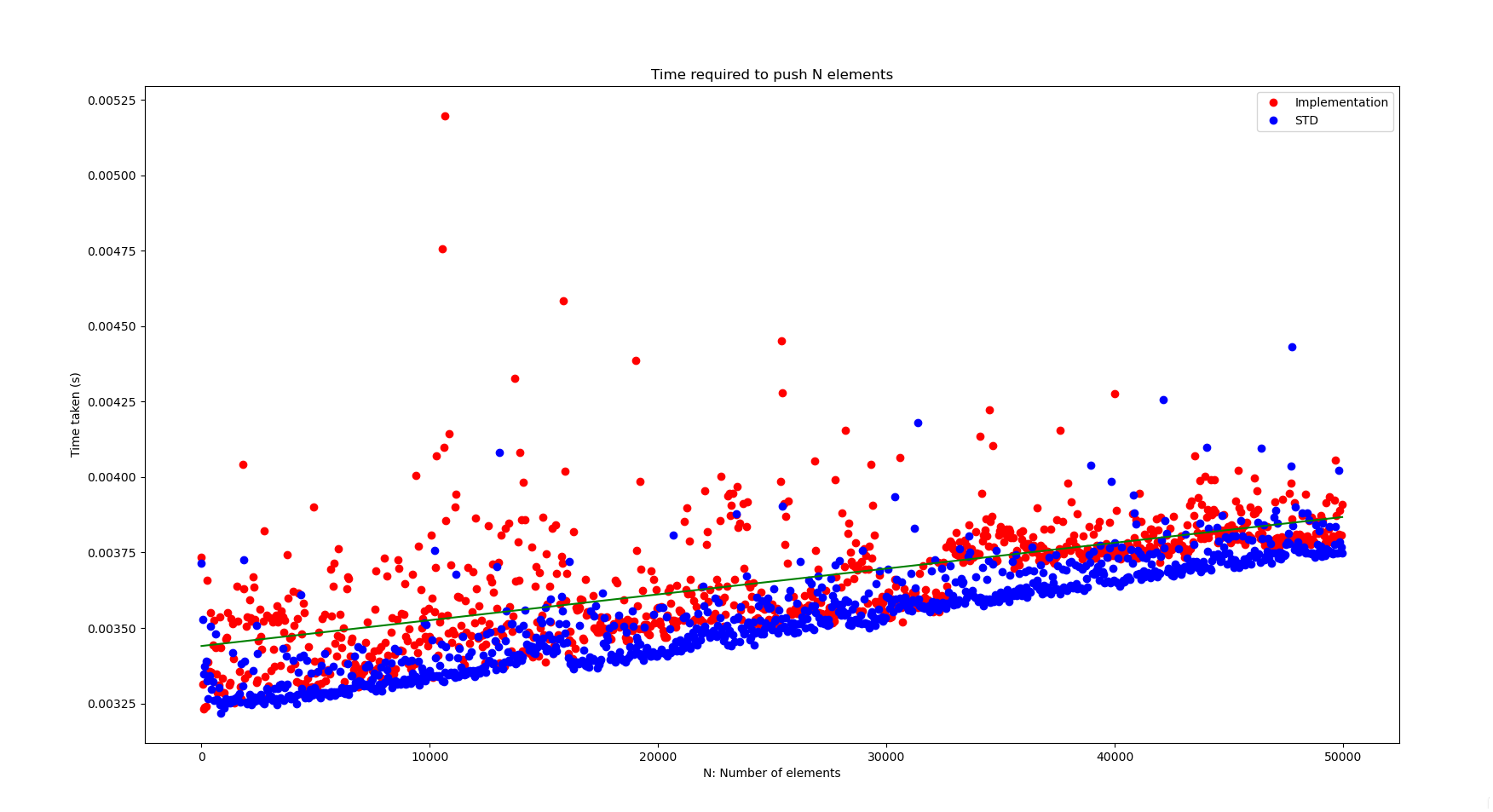
As you can see, the standard library is in general faster. But the difference is not abysmal.

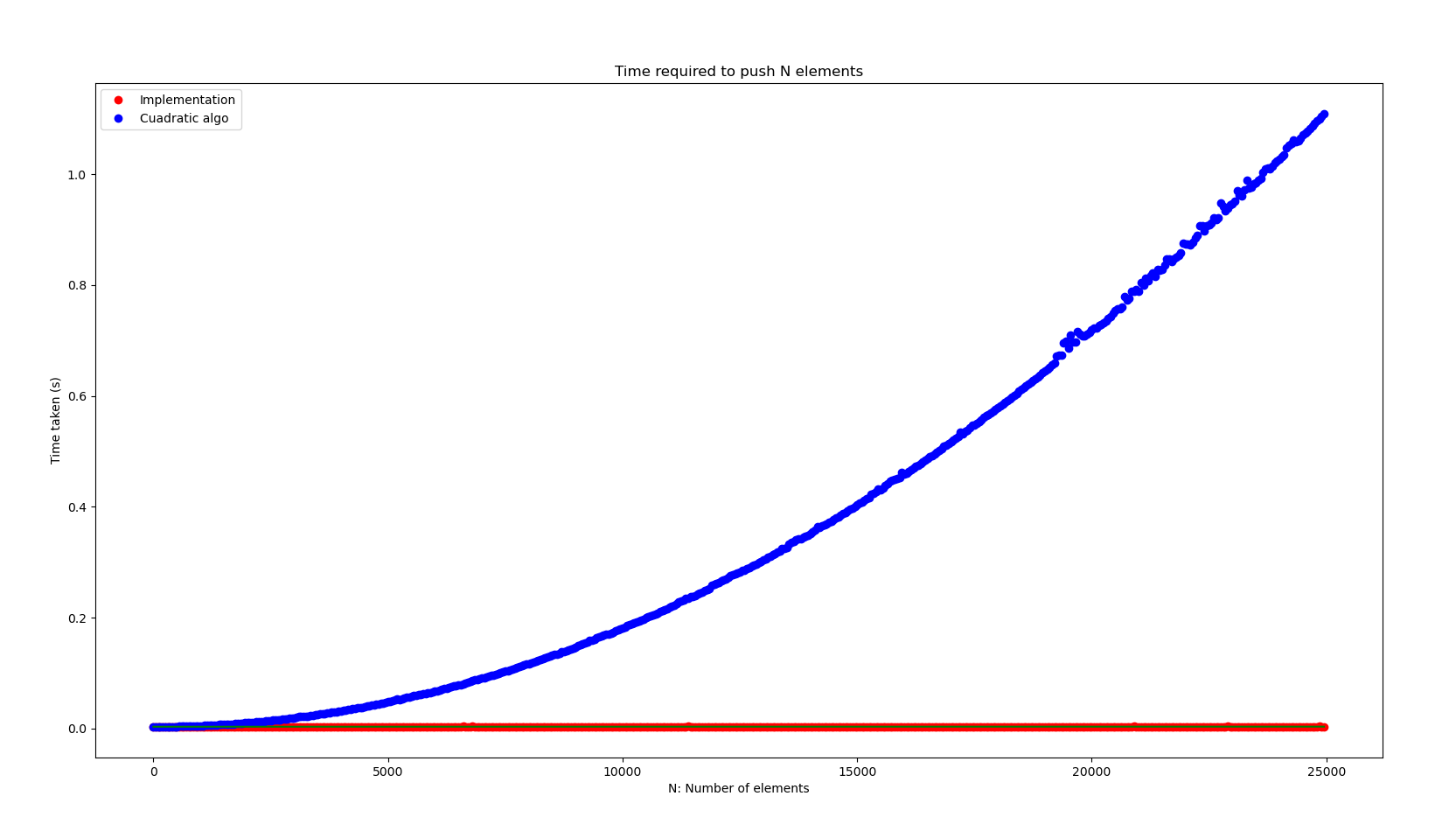
Finally, we can compare our linear runtime algorithm of inserting n elements into a stack against the following cuadratic $n^2$ algorithm.

#include <iostream>
#include <stack>
using namespace std;

int main(){
  int n; cin >> n;
  int cnt = 0;
  for (int i =0 ;i < n; i++){
    for (int j =0 ; j < n; j++){
      cnt++;
    }
  }
  return 0;
}

Here’s the comparison plot. As you’ll be able to see a cuadratic algorithm is far worse than a linear one.

Summary permalink

Wrapping up this article:

• We implemented the stack data structure in C++ using a dynamic array.
• The implementation is no much worse than the optimized standard library implementation.
• Through amortized analysis we’re able to conclude that in a dynamic array the push operation is in average $O(1)$ .