Algorithmic Problems with Tree Data Structures

Introduction permalink

In this document we’ll go over three problems solvable by using non-linear data structures. Specifically, we’re going to be using the following data-structures:

• Binary search tree (BST).
• Disjoint-set-union (DSU).
• Binary-heap.

All these data structures have in common the use of the concept of predecessor and succesor, and the intelligent use of data storing in a tree-like structure. This allows us to perform diverse operations, like inserting, and removing in better than linear ($O(n)$ ) complexity.

All the following source code will be available in my DS-course github repository.

Problem 1: K-th Lowest Element in a Binary Search Tree permalink

Given a sequence of BST insertions, our task is to find the k-th lowest element in the binary tree and its parent node. If there is no parent we must output -1.

Let’s see an example.

3 1 4 2
1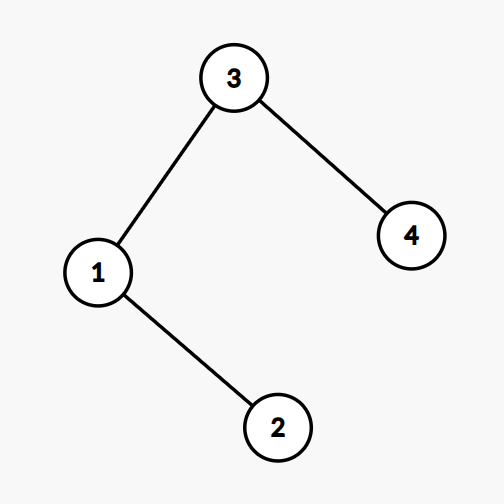

In this example we should ouput 1 3, because the 1st lowest element in the tree is one, and its parent according to the binary search tree insertions is 3.

The way to solve this problem is to implement a binary search tree or BST.

We firstly define the generic node of type T of the BST. Here’re its attributes.

• element: Element to store of type T.
• left: Left child of the node
• right: Right child of the node
• parent: Parent or ancestor of the node.

Property: Let u be a node member of the BST. All nodes v member of the tree $v < u$ go to the left of u, whereas if $v > u$ v go to the right of u.

Let’s define h as the height of the tree.

Here’re the methods of the BST data structure.

• insert(x): Insert element x in the BST O(h).
• search(x): Search key x O(h).
• remove(x): Remove key x from tree O(h).

In order to solve the problem we can simulate the insertion of the nodes into the BST.

Then we perform an inOrder traversal of the tree, that is, firstly traverse the left nodes of the subtree, process the nodes and then traverse the right part of each subtree.

If we store the nodes in this order we’ll end up having a sorted vector ans with the corresponding nodes. Then the kth answer lies in the position ans[k - 1].

This allows us not only to answer the kth-query, but up to n required queries.

Overall complexity: $O(n*h)$ , where n is the number of nodes, and h the height of the BST.

Problem 2: Infection Number permalink

This is a classic problem of set connectivity. Given an undirected graph, where each node is member of one or more components or groups, our task is to find the number of nodes reachable by the node number 0.

To solve this problem we can use the DSU data structure. Here’s its definition and methods. DSU: Data structure that solves connectivity problems and lets perform calculations of commutative operations in disjoint set

• get(u): returns id of u, O( log* n ) (iterated logarithm).
• union(u, v): merges nodes u and v O( log* n).

Then for each of the m groups of k elements we perform the union operation of the DSU between the first node and all the other ones. Note that is only necessary to perform this k times since if we make union(x, y), then if we do union(x, z), x, y, and z will be members of the same component.

We only need to modify the union operation of the data structure by introducing a size array. Each time we join two disjoint sets, we add the size of the lowest ranked (implementing the DSU with the rank heuristic), set to the higher ranked one.

It’s relevant to show here the implementation of this method.

void unionSet(int u, int v){
  int x = get(u);
  int y = get(v);
  if (x==y) return;
  if (rank[x] == rank[y]) rank[x]++; 
  if (rank[x] > rank[y]){
    par[y] = x;
    sz[x] += sz[y];
  }
  else{
    par[x] = y;
    sz[y] += sz[x];
  }
}

Then the only thing left to do is output the size of the set by doing size[get(0)].

Overall complexity using DSU: $O(n log*n)$ where n is the number of nodes and log*n the iterated logarithm.

It’s also possible to create an undirected graph using an adjacency list and perform a dfs() from the node 0. We keep a counter each time we visit a node. Then, after performing the dfs recursively we reach every reachable node by 0, thus answering the problem.

Overall complexity of second solution: $O(n + m)$ where n is the number of nodes and m the number of edges.

Problem 3: Modify sweetneess permalink

In this problem we’re asked to count the minimum number of operations required to transform the lowest element of a list of non-negative integers to be greater than or equal to k, such that $1 \leqslant k \leqslant 10^9$ , given the following operation:

• Take out the lowest (l) and second lowest (sl) numbers of the list and insert: $l + 2*sl$ .

Key observation: It’s important to show that this operation increases the minimum element of our list by at least two. This means that with a few number of operations m we’ll be able to achieve an increment of the minimum number of at least $2^m$ .

This means that if the transformation we’re required to do is possible (make the minimum element in the list greater than or equal to k) then we’ll be able to simulate it.

Inserting is a big deal in linear data structure since in average it takes linear time $O(n)$ . We’ll also need the capability of getting the minimum element from the list of numbers we’re transforming fast enough.

This is exactly what the min-heap data structure is made for. It’s not complex to implement since we’re able to represent the nodes as a contigous array of numbers.

A min-heap has the following main methods.

• push(n): Pushes element into the heap. O(log n)
• pop(): Removes and returns root element O(log n)
• top(): Return root element. O(1)

Then, to solve the problem we simply “pop out” the two smallest elements of the heap (if possible), recalculate the new element with the operation given above, and insert it again in logarithmic time. We stop as soon as the root of the min-heap is greater or equal to k.

If at any moment the size of the heap is only one and its only element is lower than k, then it’s impossible to suffice the requirement thus we must return -1.

Overall complexity: $O(n log n)$ where n is the number of element in the sequence.

Conclusion permalink

Non-linear data structures like trees allow us to perform operations like inserting and removing that have linear time in other linear data structures efficiently, by relying in a clever way to store the data and iterate through it by skipping the elements we don’t need.

With data structures like DSU, binary-heap, and BST, we’re able to solve problems in tight time constrains that would be impossible to do using linear data-structures. The problems above helped us to understand the importance of the invention of these important DSs.